画像 fibonacci sequence 0 1 1 2 3 5 308688-What is the next three terms of the fibonacci sequence 0 1 1 2 3 5
F(n2) is the number of terms in p(n), where p(n)/q(n) is the nth convergent of the formal infinite continued fraction a(0),a(1),;About List of Fibonacci Numbers This Fibonacci numbers generator is used to generate first n (up to 1) Fibonacci numbers Fibonacci number The Fibonacci numbers are the sequence of numbers F n defined by the following recurrence relationThe Fibonacci sequence begins with 0 and then 1 follows All subsequent values are the sum of the previous two, for example 0, 1, 1, 2, 3, 5, 8, 13 Complete the fibonacci () method, which takes in an index, n, and returns the nth value in the sequence Any negative index values should return 1

W 2 In The Fibonacci Sequence See How To Solve It At Qanda
What is the next three terms of the fibonacci sequence 0 1 1 2 3 5
What is the next three terms of the fibonacci sequence 0 1 1 2 3 5-C code of Fibonacci function;Fibonacci sequence formula For example F 0 = 0 F 1


Prezentaciya Na Temu 8 1 Dynamic Programming Khujaev Otabek Fibonacci Sequence Fibonacci Sequence 0 1 1 2 3 5 8 13 21 F I I If I 1 F I F I 1 F I 2 Skachat Besplatno I Bez Registracii
The Fibonacci sequence is a sequence where the next term is the sum of the previous two terms The first two terms of the Fibonacci sequence are 0 followed by 1 The Fibonacci sequence 0, 1, 1, 2, 3, 5, 8, 13, 21 Visit this page to learn about the Fibonacci sequenceIn mathematics, the Fibonacci numbers form a sequence defined recursively by = {= = > That is, after two starting values, each number is the sum of the two preceding numbers The Fibonacci sequence has been studied extensively and generalized in many ways, for example, by starting with other numbers than 0 and 1, by adding more than two numbers to generate the next number, orFibonacci numbers form a sequence 0,1,1,2,3,5,8,13,21 Using Strong Induction we can prove that f n = 1 √ 5 1 √ 5 2!
FibonacciNumbers The Fibonacci numbersare defined by the following recursive formula f0 = 1, f1 = 1, f n = f n−1 f n−2 for n ≥ 2 Thus, each number in the sequence (after the first two) is the sum of the previous two numbersThe Fibonacci sequence, also known as Fibonacci numbers, is defined as the sequence of numbers in which each number in the sequence is equal to the sum of two numbers before it The Fibonacci Sequence is given as Fibonacci Sequence = 0, 1, 1, 2, 3, 5, 8, 13, 21, Here, the third term "1" is obtained by adding first and second termN − 1 √ 5 1 − √ 5 2!
According to the Interview Cake question, the sequence goes 0,1,1,2,3,5,8,13,21 If this is the case, this solution works and is recursive without the use of arrays function fibonacci(n) { return n < 1 ?If your team was using the Fibonacci sequence to estimate the effort to develop this new widget, you would have only a few numbers to choose from at the top end of the scale 34, 55, or (This is where your Fibonacci agile scale would stop)Mar 15, 21 · Next, enter 1 in the first row of the righthand column, then add 1 and 0 to get 1 Write 1 in the column next to "2nd," then add the 1st and 2nd term to get 2, which is the 3rd number in the sequence Continue this pattern of adding the 2 previous numbers in the sequence to get 3 for the 4th term and 5 for the 5th term



Fibonacci Series In Python Python Program To Print The Fibonacci Sequence



Use Fibonacci Sequence For Table Numbers 0 1 1 2 3 5 8 13 21 34 55 144 233 377 610 Fibonacci Sequence Fibonacci Fibonacci Art
Fibonacci sequence 0, 1, 1, 2, 3, 5,?Mar 11, 21 · The Fibonacci numbers are significantly used in the computational runtime study of an algorithm to determine the greatest common divisor of two integers In arithmetic, the Wythoff array is an infinite matrix of numbers resulting from the Fibonacci sequence The Fibonacci sequence 0, 1, 1, 2, 3, 5, 8, 13, 21,It's because numbers that are too close to one another are impossible to distinguish as estimates Weber



2 Some Facts About Fibonacci Sequence 0 1 1 2 3 5 8 13 21 34 55 For N 0 For N 1 F 1 Ffor Homeworklib



Solved Recall That The Fibonacci Sequence 0 1 1 2 3 5 Chegg Com
Related to the Fibonacci sequence is another famous mathematic term the Golden RatioWhen a number in the Fibonacci series is divided by the number preceding it, the quotients themselves become a series that follows a fascinating pattern 1/1 = 1, 2/1 = 2, 3/2 = 15, 5/3 = 1666, 8/5 = 16, 13/8 = 1625, 21/13 = , 34/21 = 1619, 55/34 = , andThe Fibonacci Numbers The numbers are 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, , 144, 233, 377, Each Fibonacci number is the sum of the previous two Fibonacci numbers!Sep 10, 19 · The traditional Fibonacci sequence is 1, 2, 3, 5, 8, 13, 21 and so on, with each number the sum of the preceding numbers Years ago I began having teams estimate with a modified Fibonacci sequence of 1, 2, 3, 5, 8, 13, , 40 and 100 Why?



W 2 In The Fibonacci Sequence See How To Solve It At Qanda



Fibonacci Numbers 0 1 1 2 3 5 8 13 21 34 55 144 233 377 610 987 1597 2584 4181 6765 Ppt Video Online Download
Fibonacci's Solution The Fibonacci Sequence!See the picture below which explains the fibonacci spiral The number 1 in the sequence stands for a square with each side 1 long The number 2 stands for a square of 2 by 2 and so on If the sides of the square are placed next to each other a new side of a larger square forms as explained before, eg 23 gives 5 and same goes for the squaresThe problem yields the 'Fibonacci sequence' 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, , 144, 233, 377 Fibonacci omitted the first term (1) in Liber Abaci The recurrence formula for these numbers is F (0) = 0 F (1) = 1 F (n) = F (n − 1) F (n − 2) n > 1 Although Fibonacci only gave the sequence, he obviously knew that the nth number of his sequence was the sum of the two previous numbers



19dfvdvf By Dfvdfbeerer Issuu



Fibonacci Numbers 0 1 1 2 3 5 8 13 21 34 55 144 233 377 610 987 1597 2584 4181 6765 Ppt Video Online Download
Jul 15, 19 · 3 is calculated by adding the two numbers preceding it (12), 5 is (23), and so on Here is an example of Fibonacci series 0,1,1,2,3,5,8,13etc In the above example, 0 and 1 are the first two terms of the seriesFeb 11, 18 · The Fibonacci numbers are the numbers in the following integer sequence 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, , 144,The Fibonacci sequence is a series where the next term is the sum of pervious two terms The first two terms of the Fibonacci sequence is 0 followed by



Solved The Fibonacci Sequence Is The Series Of Numbers 0 Chegg Com



Solved The Fibonacci Sequence Is 0 1 1 2 3 5 8 13 Chegg Com
The first number in the Fibonacci sequence is 0, the second number is 1 The subsequent number is the result of the sum of the previous two eg, the third number 1 = 10, the fourth number 2=11, the fifth number 3 = 21 The Fn number is defined as follows Fn = Fn1 Fn2, with the seed values F0 = 0, F1 = 1 C Programs for Fibonacci SeriesThis preview shows page 8 13 out of 18 pages Terms = 2 Fibonacci sequence = 5, 8 Ratio pair 1 = Fibonacci sequence = 5, 8 Ratio pair 1 =1)what is the degree of polynomial equation 2x³11x²x4=0?



Fibonacci Series Formative Project Report Essay Type



Fibonacci Series In Java Program 4 Multiple Ways
2 C 2 2 C0 3 C 1 3 C 2 3 C 3 3 C0 4 C 1 4 C 2 4 C 3 4 C 4 4 In this version of Pascal's triangle, we have Ci j = k!It means, (Fibonacci_series(0) Fibonacci_series(1)) return (0 1) = return 1 NOTE For Recursive functions, it is very important to place a condition before using the function recursivelyFibonacci Series generates subsequent number by adding two previous numbers Fibonacci series starts from two numbers − F 0 & F 1The initial values of F 0 & F 1 can be taken 0, 1 or 1, 1 respectively Fibonacci series satisfies the following conditions −



Fibonacci Number Wikipedia
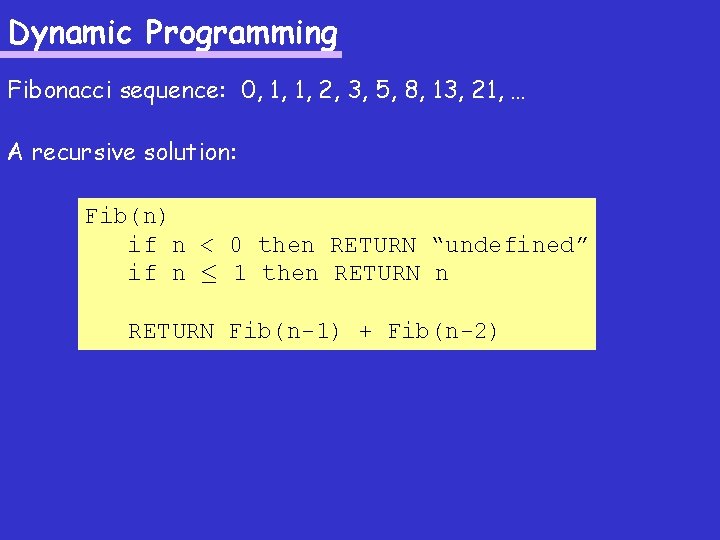


Dynamic Programming Fibonacci Sequence 0 1 1 2
I!(k )!, where i represents the column and k represents the row the given term is in Obviously, we have designated the rst row as row 0 and the rst column as column 0 Finally, we will now depict Pascal's triangle with itsLeonardo Bonacci also known as Leonardo Fibonacci (which is a nickname to say son of Bonacci), has created one of the most fascinating series in our universe using simple addition techniques while observing rabbit populations Now, to be fair, theAug 01, · Enter how many numbers needed in Fibonacci series – 6 0,1,1,2,3,5, Python Program for Fibonacci Series using recursion Create a recursive function which receives an integer as an argument This integer argument represents the position in Fibonacci series and returns the value at that position Thus, if it receives 5, it returns the value at



Solved Problem 2 8 Pts Fibonacci Sequence Series Numbers 0 1 1 2 3 5 8 Formally Expressed Fib0 0 Q



Mathematician Correction In Post Refer The Latest Post Or Comment Section Formula Is F N Phi N 1 Phi N 5 Leonardo Fibonacci Or Leonardo Of Pisa Was A Mathematician From
Feb 26, · In mathematics, the Fibonacci numbers are the numbers in the following integer sequence, called the Fibonacci sequence, and characterized by the fact that every number afterSep 11, · Fibonacci Series is a pattern of numbers where each number is the result of addition of the previous two consecutive numbers First 2 numbers start with 0 and 1 The third numbers in the sequence is 01=1 The 4th number is the addition of 2nd and 3rd number ie 11=2 and so onThe Fibonacci sequence obeys the recursion relation P(n) = P(n1) P(n2) In such a sequence the first two values are arbitrarily chosen They are called the "seeds" of the sequence When 0 and 1 are chosen as seeds, or 1 and 1, or 1 and 2, the sequence is called the Fibonacci sequence



Solved 3 The Fibonacci Numbers Are The Numbers In The Fo Chegg Com



Fibonacci Sequence Arithmetic Mathematical Notation
The Fibonacci sequence is a series of numbers where a number is the sum of previous two numbers Starting with 0 and 1, the sequence goes 0, 1, 1, 2, 3, 5, 8, 13, 21, and so on Here we will write three programs to print fibonacci series 1) using for loop 2) using while loop 3) based on the number entered by userMath problems 2pdf FIBONACCI NUMBERS GET INTO EVERYTHING(0 1 1 2 3 5 8 13 21 34 55 144 233 377 610 987 1597 The Fibonacci sequence may be definedEg, p(3) = a(0)a(1)a(2)a(3) a(0)a(1) a(0)a(3) a(2)a(3) 1 has F(5) terms Also, F(n1) is the number of terms in q(n) Clark Kimberling, Dec 23 15


What Is The Pattern Of Sequence 1 1 2 3 5 8 13 Quora



Ppt Math In Nature Powerpoint Presentation Free Download Id
Fibonacci sequence is a sequence of numbers where the next number is the sum of the previous two numbers behind it It has its beginning two numbers predefined as 0 and 1 The sequence goes on like this 0,1,1,2,3,5,8,13,21,34,55,,144,233,377 UsageOct 02, 17 · Using The Fibonacci Sequence With Your Team To use the Fibonacci Sequence, instruct your team to score tasks from the Fibonacci Sequence up to 21 1, 2, 3, 5, 8, 13, 21 One being the smallest easiest tasks and twentyone being large projectsWhat is the next term?



Wk7 51 Algorithm Fibonacci Sequence 0 1 1 2 3 5 8 13 31 35 N Youtube



Effective Algorithm For N Fibonacci Number By Professor Lili Saghafi
Fibonacci sequence is a sequence of numbers, where each number is the sum of the 2 previous numbers, except the first two numbers that are 0 and 1 Fibonacci sequence formula;Feb 14, 21 · Enter number of terms 10 0 1 1 2 3 5 8 13 21 34 Printing Nth term of Fibonacci series using recursion Accept a number of a term from the user and pass it to theThe fibonacci sequence is a famous bit of mathematics, and it happens to have a recursive definition The first two values in the sequence are 0 and 1 (essentially 2 base cases)



Fibonacci Number Wikipedia



Fibonacci 60 Code Jain 108
Sep 23, 19 · Fibonacci series is a series of numbers formed by the addition of the preceeding two numbers in the series Example of Fibonacci Series 0,1,1,2,3,5 In the above example, 0 and 1 are the first two terms of the series These two terms are printed directlyWhat is the Golden Ratio?Apr 11, 21 · Source code to print fibonacci series in pythonSolve fibonacci sequence using 5 Method 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ,



Technology Analysis Of Python Classic Interview Questions Implementing The Fibonacci Sequence Programmer Sought



Fibonacci A Series Of Numbers That Can Prove The Existence Of God
Oct 03, 14 · The Fibonacci numbers are a fascinating sequence of numbers We can generate the sequence in various ways Let's use some special cases to generate the Fibonacci sequence Case 1 (Iterative Approach) This approach is the simplest and quickest way to generate the sequence of Fibonacci NumbersThe Fibonacci sequence is 0, 1, 1, 2, 3, 5, 8, 13, 21, where the first two terms are 0 and 1, and each term thereafter is the sum of the two preceding termsThe Fibonacci numbers are generated by setting F 0 = 0, F 1 = 1, and then using the recursive formula F n = F n1 F n2 to get the rest Thus the sequence begins 0



Fibonacci Numbers Fibonacci Numbers Fibonacci Numbers 0 1 1 2 3 5 8 13 21 34 Where Each Number Is The Sum Of The Preceding Two Recursive Ppt Download
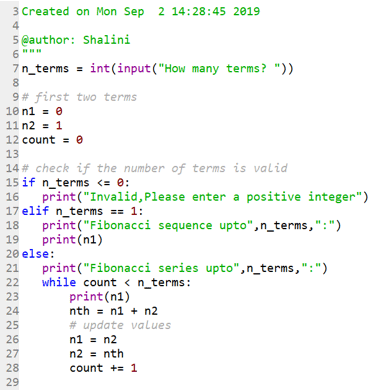


Fibonacci Series In Python Methods Numbers And Series
Fibonacci Series in C Fibonacci Series in C In case of fibonacci series, next number is the sum of previous two numbers for example 0, 1, 1, 2, 3, 5, 8, 13, 21We can easily remember Fibonacci Sequence using the Fibonacci Day, which is November 23rd As 23rd November has the digits "1, 1, 2, 3" which is part of the sequence In the above image, the first two numbers are 0 and 1 So, according to the Fibonacci rule the third number is 1 (sum of 0 and 1) The fourth number is 2 and so onJan , 21 · The Fibonacci numbers are the numbers in the following integer sequence 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, , 144, In mathematical terms, the sequence Fn of Fibonacci numbers is defined by the recurrence relation F n = F n1 F n2



The Paras World School Put Your Math Knowledge To The Test By Taking This Quiz Question What Is The Next Number In The Fibonacci Sequence 0 1 1 2 3 5



W 2 In The Fibonacci Sequence See How To Solve It At Qanda
N, for n= 0,1,2, Proof Let P(n) be the statement that this formula is true, where n≥ 0 (Base Case) We first show P(0) and P(1) are true, ie that the formula is valid when n= 0 andLet n any positive integer If F n is what we use to describe the nth Fibonacci number, then F n = F n−1 F n−21, 1, 2, 3, 5, 8, 13, 21, 34, 55, , 144, So, at the end of the year, there will be 144 pairs of rabbits, all resulting from the one original pair born on January 1 of that year Each term in the Fibonacci sequence is called a Fibonacci number


The Numbers Of Nature The Fibonacci Sequence Eniscuola



Math In Nature A B Golden Ratio 1 618 Fibonacci Sequence 0 1 1 2 3 5 8 13 21 34 9gag



Write A Program In Python To Display Fibonacci Series 0 1 1 2 3 5 8 Brainly In



The 8th Term Of The Sequence 1 1 2 3 5 8 Is



Calameo Fibonacci Numbers And The Golden Section Pdf



Pin Ot Polzovatelya Amy Nichols Na Doske 41 Fibonacci Zolotoe Sechenie Sakralnaya Geometriya Geometriya



1 In The Fibonacci Sequence 0 1 1 2 3 5 8 What Is The Value Of Fs F5 5 F5 3 F5 Brainly Com



An Introduction To Fibonacci Series Ipem



C Program For Fibonacci Numbers With And Without Recursion Discoverbits



Fibonacci Series In Python Program Using Loops Recursion Edureka
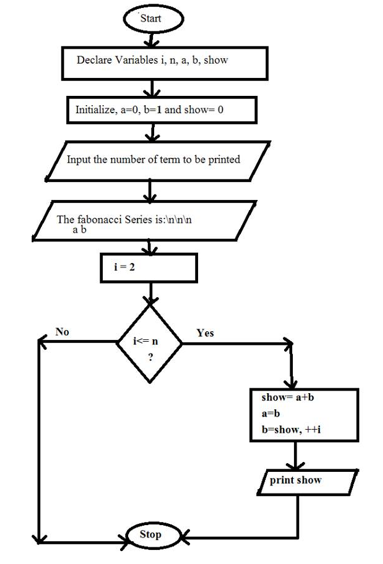


Fibonacci Series Algorithm And Flowchart Code With C



C Program To Display Fibonacci Series Using While Loop


What Is The Pattern Of Sequence 1 1 2 3 5 8 13 Quora



Cs3161 Operating System Principles



Fibonacci Sequence



Fibonacci Numbers Consequences Of Fibonacci Numbers How Many



구로희 Fibonacci Sequence 0 1 1 1 1 2 1 2 3 2 3 5 3 5 8 5 8 13 See The Spiral Everything Starts From 0



Solved Let Us Recall That The Famous Fibonacci Sequence Chegg Com



0 1 1 2 3 5 8 13 21 34 55 Scientific Scribbles



Guru Nanak Institution What Are The Next Numbers In The Fibonacci Sequence 0 1 1 2 3 5 8 13 21 34 Quiz Arithmetic Arithmeticquiz T Co 1npiir0rcx



Fibonacci Numbers Consequences Of Fibonacci Numbers How Many



Program For Fibonacci Numbers Geeksforgeeks



Math In Flowers Symmetry Fibonacci And A Fun Video Shade Metals



Ppt Introduction To Fibonacci Number In Mathematics The Fibonacci Numbers Are The Numbers In The Powerpoint Presentation Id


Prezentaciya Na Temu 8 1 Dynamic Programming Khujaev Otabek Fibonacci Sequence Fibonacci Sequence 0 1 1 2 3 5 8 13 21 F I I If I 1 F I F I 1 F I 2 Skachat Besplatno I Bez Registracii



Fibonacci Sequence Discrete Mathematics Applied Mathematics



Answered Write A Program In Java To Display Bartleby



2 Some Facts About Fibonacci Sequence 0 1 1 2 3 5 8 13 21 34 55 For N 0 For N 1 F 1 Ffor Homeworklib



The Fibonacci Sequence Youtube



Slides Show



Amazon Com Fibonacci Appstore For Android



Solved Assignment 5 1 Given The Fibonacci Sequence 0 1 Chegg Com



9 Based Tuning Sounds Of Silence


Golden Rectangle The Gold Box Is A Box With Proportions Which Are Two Download Scientific Diagram
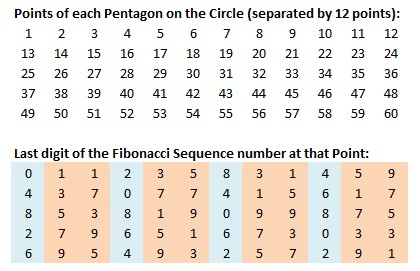


Fibonacci 60 Repeating Pattern The Golden Ratio Phi 1 618



Fibonacci Series Php Php Lines For Fibonacci Series With 2 Approaches



Solved One Amazing Sets Numbers Set Called Fibonacci Numbers Set Numbers Begins 0 1 1 2 3 5 8 13 Q
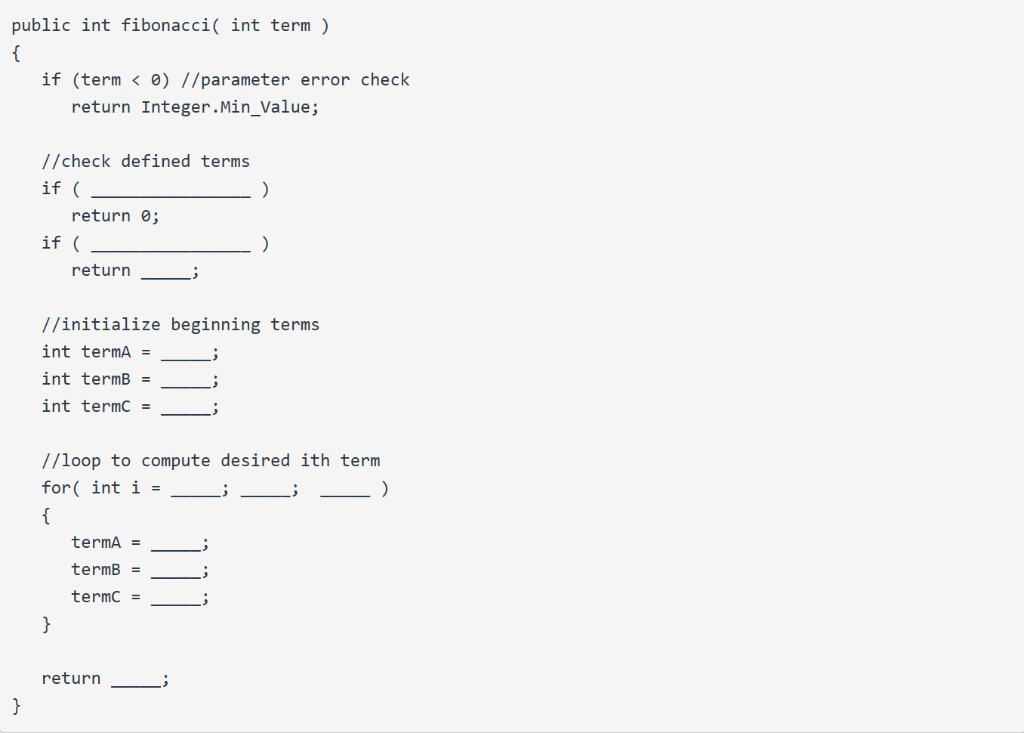


Solved Java Mathematics Fibonacci Sequence Numbers Following Integer Sequence 0 1 1 2 3 5 8 13 21 Q



Program Of Fibonacci Numbers Method 1 Dev Community



F Fibonacci Sequence Fibonacci



Fibonacci Series Program In C



Fibonacci Numbers Coolgyan Org



Pin On Something Naturally Curious



Fibonacci Series Program In Java


What Is The Next Number In The Sequence 0 1 1 2 3 5 Quora


Answered In The Fibonacci Sequence 0 1 1 2 Bartleby
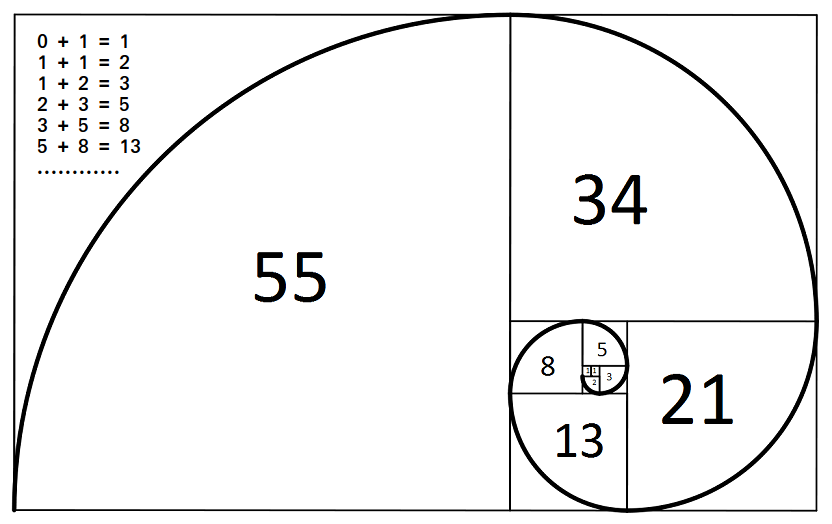


Program To Print First N Fibonacci Numbers Set 1 Geeksforgeeks



Fibonacci Sequence



How To Design A Logo With Golden Ratio Spiral By Dainogo Linkedin
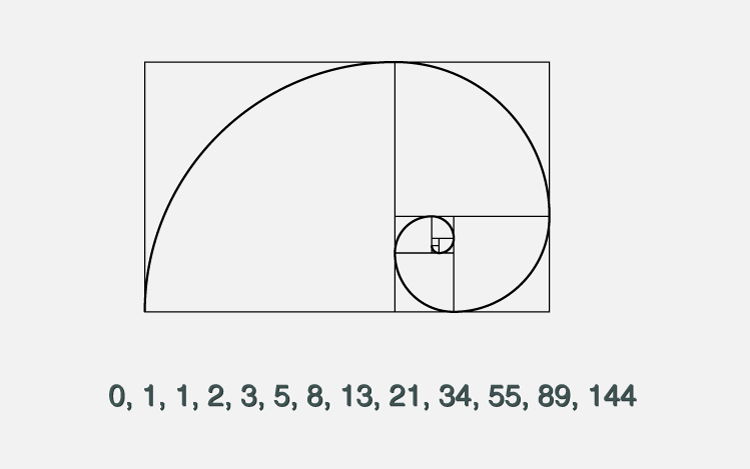


C Program To Display Fibonacci Sequence Devops Tech



Things You Didn T Know About The Fibonacci Sequence Vincit


Fibonacci



The Fibonacci Numbers Start With Fo 0 F1 1 1 F2 Etc 0 1 1 2 3 5 8 13 21 34 55 144 233 377 Show Tha Homeworklib



Program To Display Fibonacci Series 0 1 1 2 3 5 8 13 21 34 55 Fibonacciseries Crpogramming Youtube
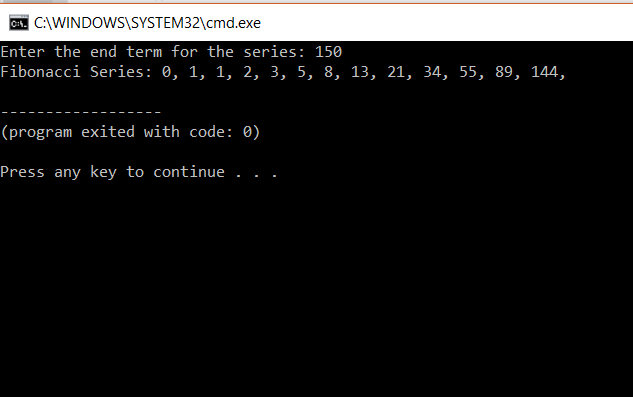


Fibonacci Series In C Edureka



Using A Switch Statement Write A Menu Driven Program To A Generate And Knowledgeboat


Dynamic Programming Fibonacci Sequence 0 1 1 2
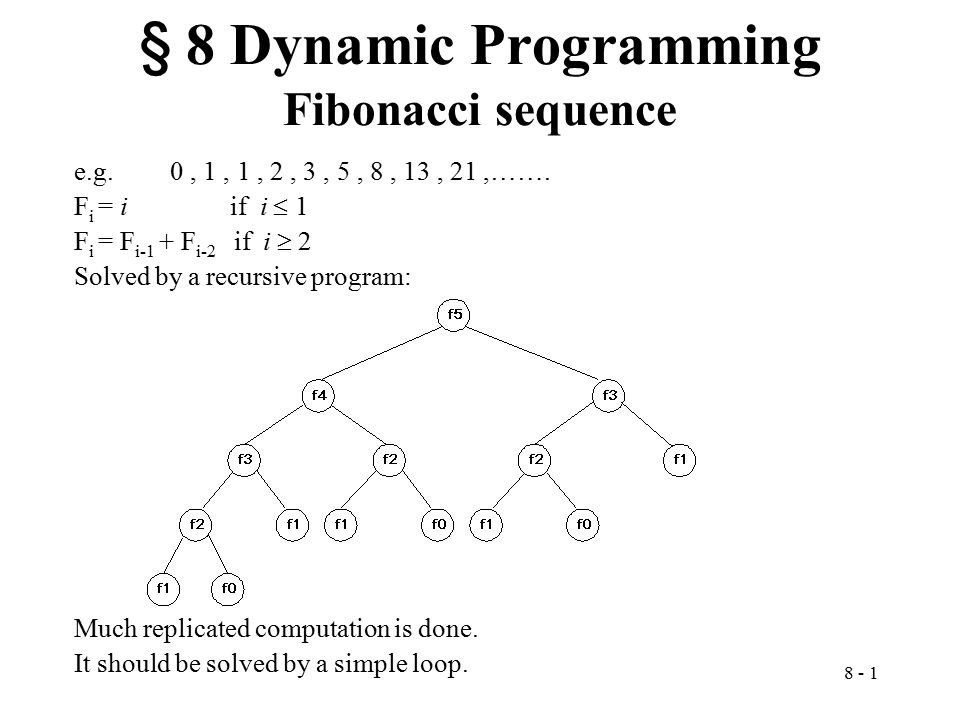


8 Dynamic Programming Fibonacci Sequence Ppt Video Online Download



Fibonacci Sequence Lecture L 10 1 Section 10
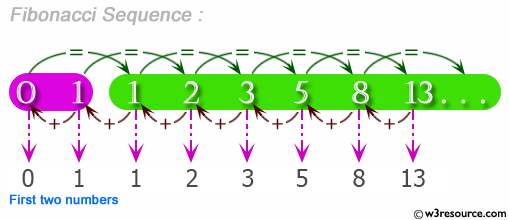


Python Exercise Fibonacci Series Between 0 To 50 W3resource



Pdf Generalized Fibonacci Numbers Cosmological Analogies And An Invariant



The Fibonacci Sequence Is The Sequence 0 1 1 2 3 5 8 13 21 Writ



Fibonacci Numbers Of Sunflower Seed Spirals Stock Photo Image By C Khunta



Solved Fibonacci Numbers Are 0 1 1 2 3 5 8 13 21 Chegg Com



What Is The Fibonacci Sequence Fibonacci Sequence Fibonacci Fibonacci Spiral


Cse370 Final Exam Solution



Fibonacci Series Program In Java


How To Generate Fibonacci Sequence In Python Laptrinhx
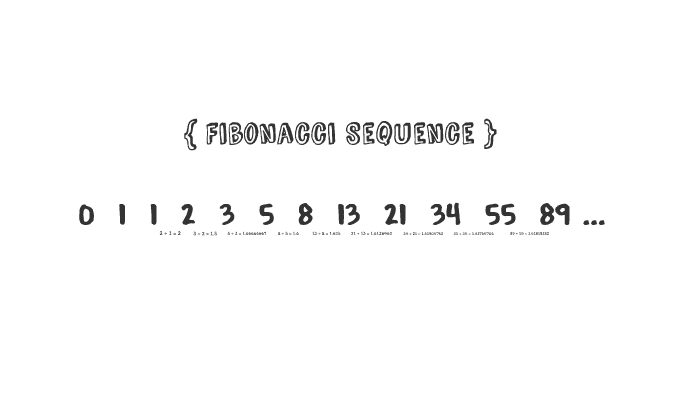


0 1 1 2 3 5 8 13 21 34 55 144 By 진영 이



C Programming Print Fibonacci Series 0 1 1 2 3 5 8 Cute766


コメント
コメントを投稿